common cathode 회로의 신호처리적인 해석 방법

위 그림은 기타 앰프 회로의 주를 이루는 common cathode 회로이다. 기타앰프 회로를 보다 보면 이것은 마치 어떤 관용구처럼 쓰여지는 패턴이다. 자꾸 보다보면 나도 쉽게 만들 수 있을 것 같단 생각이 든다. 어떤 이론이라든가 어려운 지식을 가지고 만들어진게 아니란 게 느껴진다. 대부분은 R/C를 계속 바꿔 달고 실험하다 보니 ‘이 소리가 굳인겨!’ 하고 얻어진 회로이다. 전통의 패턴 두 가지를 가지고 이래 저래 응용해 먹은 것이다.

그러나 실시간 플러긴 형태로 이것을 흉내내려면 진공관이라는 요소 때문에 골치가 된다. R과 C만으로 구성된 회로는 쉽게 계산해서 똑같이 시뮬레이션할 수 있다. 오히려 실제 회로보다 더 정확하게 돌아간다. 실제 회로는 여러 가지 오차들이 많이 있으니까 말이다. 좋은 부품이고 나쁜 부품이고 따질 필요도 없다. 디지털 세계에서는 거의 칼과 같이 정확하게 돌릴 수 있다.

본론으로 돌아와서, 그림의 회로를 보면 진공관을 빼면 오직 R과 C로만 되어있다. 진공관 모델은 인터넷에도 잘 돌아다니고 있을 정도로 잘 알려져있다. grid current, plate current 모두 grid-cathode voltage와 plate-cathode voltage의 함수로 나타난다. 즉 이 회로는 이 함수까지 모조리 빼내서 방정식을 풀어주어야 close form의 해를 얻을 수 있다. 그러나 쉽지 않다. 그래서 이 회로를 풀어주는 다른 방법을 강구해야 되는 것이다.

일반적인 방법으로 이 회로를 풀려면 3단자 (grid/cathode/plate)에 해당하는 전압을 대략적으로 구하고 그 다음 진공관 모델을 적용해서 전류값을 계산하고 그것을 다시 주변의 RC에 적용해서 3단자의 전압을 구하고 전류를 구하고 하는 과정을 반복해서 가장 근사한 값을 계산해야 한다. 멍청하게 이 과정을 반복하면 해를 찾지 못하고 해 주위를 서성이는 결과를 얻게 되므로 머릴 써서 해에 수렴하도록 수치해석적인 방법을 이용해야 한다.

역시나 이것을 실시간으로 게다가 최소 1초에 4만4천100번씩 계산해내야 한다. aliasing을 피해서 음질을 올려주려면 2배 4배 8배 더 자주 계산해내야 한다. 아무리 컴퓨터가 좋아졌어도 실시간으로 이 계산만시키면 컴퓨터는 매우 힘들어한다. 다른 일을 하기 어려워진다.

다음의 블록 다이어그램은 실시간으로 회로 시뮬레이션을 가능하게 만들기 위해서 여러 사람들이 고민해낸 결과 끝에 만들어낸 것이다.

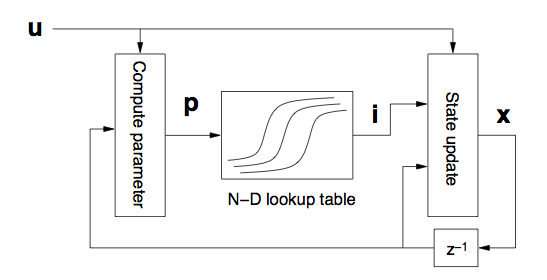
그림은 다음과 같이 해석할 수 있다.

1) 회로에는 상태 변수가 존재한다. 회로에서 기억소자 노릇을 하는 C 양단간의 전압이 그것이다 (L의 경우라면 전류가 그 역할을 할 것이다).

2) 새로운 입력 u에 대해서 상태변수 변경

3) 상태변수를 통해 비선형 소자의 출력을 계산 (비선형 함수는 lookup table로 대체)

4) 상태변수 업데이트

State space로 어떤 시스템을 모델링하는 것은 꽤나 고전적인 접근 방법인데, 기본적으로 state space로 어떠한 시스템을 분석하는 것은 1) 현재 상태변수와 현재의 입력을 통해 상태변수의 변화량(differentiate)을 계산, 2) 과거의 상태변수와 현재의 입력을 통해 현재의 시스템 출력을 계산하는 것이다. 지금의 이 비선형 시스템을 분석하는 방법은 nonlinearity를 반영하기 위해서 어떤 table lookup (또는 복잡한 비선형 function call)이 들어간 차이만 있을 뿐이다. 즉, 과거의 상태변수와 현재 시스템의 입력을 통해 변화량을 계산하지 않고 비선형 소자의 입력을 계산하고 그것을 바탕으로 현재의 상태변수를 업데이트하는 방법으로 분석하는 것이다.

이 방법에 있어서 기존의 방법 (내가 사용한 접근 방법)과의 차이점이라고 하면

• 획일화된 filtering 방법을 사용하지 않음: 회로를 간단히 분석하고 그 응답특성을 가지고 bilinear transform한 뒤 표준화된 filter를 통해서 시변 특성을 반영하는 방법이 아니라 말 그대로 회로 상에서 기억소자 노릇을 하는 C를 상태변수로 하여 입력이 일으키는 상태변화를 반영한 결과를 비선형 함수에 넣고 그 결과를 다시 상태변수 업데이트하는 반복과정이 된다.

• 회로를 모두 통째로 분석해야 함: KVL이라든가 KCL을 통해서 상태 변수가 update되는 수식을 유도하고 이것을 행렬식으로 만드는 것으로 모든 과정은 끝난다. 어차피 회로에 들어가는 부품값은 대부분 고정이므로 불필요하게 매번 bilinear transform할 필요도 없고 다차의 filter를 만들 필요도 없고 사실상 회로 시뮬레이션에 필요한 최소한의 식을 가지고 운영하게 되므로 계산과정도 매우 줄어들게 된다. 다만 분석결과는 복잡한 꼴이 되는데, 어차피 몇 가지 패턴에 대해서 분석 결과를 가지고 있으면 다양하게 응용이 가능하다. 쉽게 말해서 어떤 회로가 주어졌을 때 이것을 모델링하는 과정은 자동화가 가능하다. 반면 기존에 사용하던 방법을 쓰면 case-by-case로 filter function call이 이루어지므로 다분히 조립식을 만들어가는 기분으로 모델링을 할 수 있으나, 정확도는 stage가 늘어날 수록 점점 떨어지게 된다.

뭐 어쨌든 결과만 놓고보면 다음과 같은 수식을 얻어낼 수 있다.

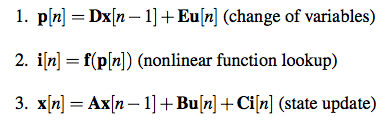
위 수식이 전부 행렬식인 것은 우리가 다루는 상태변수가 하나가 아닌 여러 개이고 그것들이 mesh equation으로 얻어지는 것들이라 그렇다. 수식에서 보는 바와 같이 과거 상태에 새로운 입력이 영향을 주어 비선형 소자를 driving하는 value를 얻는 부분, 또 그 value를 바탕으로 비선형 소자의 출력을 얻어내는 부분, 그리고 비선형 소자의 출력이 적용되어 상태변수가 업데이트되는 부분으로 나뉘어진다.

이 방법을 쓰면 수치해석을 쓰는 spice와 거의 같은 수준의 정확도를 얻을 수 있으면서도 상대적으로 계산량이 작고, 회로만 보고도 곧바로 수식으로 옮길 수 있는 수준의 응용 용이함을 가지고 있어서 다양한 회로를 simulation하기에 상대적으로 유리하다는 장점이 있다. 이것도 결국 더욱 간략하게 만들어보면 내가 여태 사용하던 모델링 방법과 크게 다르지 않다.

즉 심플한 비선형 모델 (table look-up에 비해서는 살짝 많은 연산을 사용하나 memory는 거의 사용하지 않는)과 여러 가지 IIR filter를 쓰는 과정은 state space model을 써서 R, C filter의 효과를 얻어내는 것이나 같다. 다만, 비선형 모델을 심플하게 가져가기 위해서 실제 회로의 동작과 완벽하게 일치시키지는 않는다는 차이는 있다.