Sigmoid Function
on
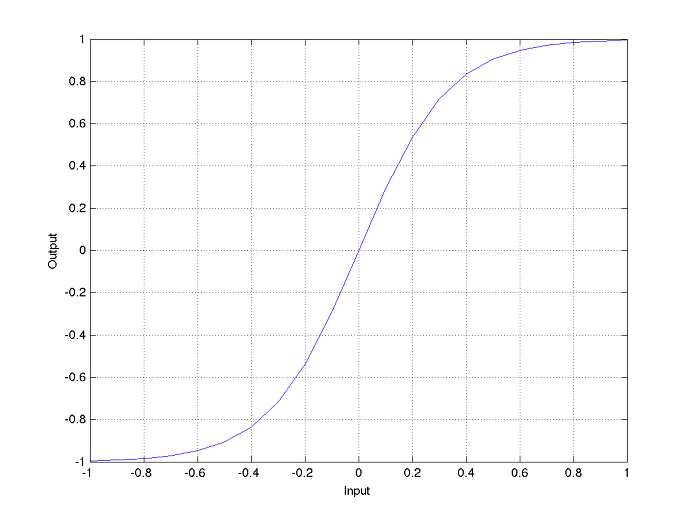
Sigmoid function이라는 일종의 비선형 함수가 있다. exponential function을 살짝 이용해서 비선형성을 갖도록 만든 함수인데, 이게 의외로 전자공학 분야에서는 많이 쓰이는 함수이다.
신경망(Neural Network)라고 들어봤는가? 한동안 엄청 뜨다가 지금은 어디갔는지 종적을 알 수 없는 분야인데, 기 정말 논문 쓸 거리가 없을 때 꺼내서 잘근 잘근 씹어주는 그런 분야가 있다. 그러다가 갑자기 기적적으로 부활하여 deep-learning이라고 해서 예전보다 훨씬 복잡한 구조로 구현되면서 인공지능의 총아로 발돋움하고 있다.
이것은, 쉽게 말해서 뇌가 어떤 자극을 받아들일 때 fuzzy한 특성, 즉 1도 아니고 0도 아닌 애매한 응답을 해준다는 것에 근거하여 확실한 사실들에 대하여 강제로 학습을 시키고, 이도 저도 아닌 애매한 입력이 들어왔을 때 그 학습된 기억을 바탕으로 fuzzy한 출력을 내주도록 만들어놓은 것이다. 이것을 마구잡이로 서로 연결해 놓으면 학습효과에 의하여 복잡한 입력에 대해서도 어느 정도 신빙성있는 출력을 내어준다는 아이디어다. 글로 적으려니 이해하기가 쉽지 않겠지만 뭐 일단 그렇다는 얘기다. 실제로 이 분야는 어떤 이론적인 증명이라든가 딱 떨어지는 수식으로 파는 접근이 어려워서 늘상 특정 케이스에 대해서 실험해봤더니 좋더라 좋아지더라의 논문만이 난무하는 분야라 그저 부지런히 실험 많이 하고 좋아지는 케이스를 찾을 때마다 논문써서 실적 올리는 데는 좋은 쓰임새가 있다고 할 수 있다 (라고 하면 그 분야를 전공한 사람들에게 돌팔매질을 당하겠지만 다들 그렇게 이해하고 있다).
이 신경망에서 쓰는 ‘1도 아니고 0도 아니여’의 응답을 가져다 주는 기능을 이 sigmoid function에 의지한다. 진공관을 시뮬레이션 하자는 이 마당에 왜 sigmoid function을 끄집어냈느냐 할 수 있다. 아래 그림을 보자.

이 그림은 sigmoid function을 적당히 손봐서 입력대비 출력의 그림을 나타낸 것이다. sigmoid function은 입맛에 맞춰 사실 조작하기 나름이다. 어떻게 사용하느냐가 중요할 따름인 거다.
그림에서 보다시피 입력이 증가하면 어느 수준을 넘어서면 더 이상 증가하지 않는 특성을 갖는다. 그런데 칼같이 구부러지지 않고 부드럽게 구부러지는 특성을 갖기에 우리는 이것을 soft clipping이라고 하는 것이다. soft clipping하면 뭐가 좋냐 물어볼 수 있는데, 귀에 거슬리는 3rd, 4th harmonic보다 2nd order harmonic이 많이 증가하게 된다.
하모닉이 좋고 나쁜 것에 대해 얘기하자면, 좀 무식하게 들릴지 모르겠지만 이렇게 이해하면 빠를 것 같다. 어떤 음의 주파수가 있을 때, 그 주파수의 2배가 되면 1 옥타브 높은 소리가 된다. 음악시간에 잘 배웠겠지만 1옥타브 높은 소리는 완전 음정으로 (perfect interval) 그 울림이 지저분하지 않고 완벽해진다. 여기에 다시 두배를 하면 원래 음의 2옥타브 높은 소리가 된다. 역시 그 울림이 완벽하다. 그런데, 원래 음의 주파수의 3배가 되면 1옥타브 높은 완전 5도 음정이 된다. 즉 ‘도’를 찌그러뜨리면 한 옥타브 높은 ‘솔’이 섞여 들어간다는 말이다. 역시 완전 5도라 울림은 좋다, 그렇지만 5차는 좀 애매한 음정이 된다 (2옥타브 높은 단 3도?). 어쨌든 하드하게 클리핑을 하면 2차 배음은 거의 보기 힘들고 3차 이상의 하모닉만 많아지고, 그 각각의 하모닉도 순수한 하모닉이라기 보단 주변에 다른 배음을 가지고 있다. 따라서, 디스토션이 마냥 심하게 일어난다고 좋지 않은 것처럼 쓸데없이 소리의 에너지가 울림이 좋지 않은 쪽으로 흩어지게 된다는 뜻도 아울러 된다.
즉하드 클리핑이 일어나면 순수한 완전 5도 8도 음정만이 아닌 애매한 음정의 배음들이 늘어나게 되어 소리의 에너지는 같다고 하더라도 음의 전달은 불명확해진다는 뜻 되시겠다. 사실상 귀를 짜증나게하는 간섭(=잡음)으로 볼 수 있다는 얘기다. 그래서 TR 혹은 diode clipping이 안좋다 떠들고 Tube가 좋다 하는 것이다.
Tube에서 왜 2nd order harmonic이 늘어나는가에 대해서는 이미 얘기한 바가 있다. grid limiting current에 의해서 입력단에서 신호가 찌그러지는데 그 모양이 매우 완만해서 3rd보다 2nd가 많이 늘어난다는 얘기인 것이다.
위 그림의 sigmoid function에 sine wave를 넣어주면 어떻게 될까 spectrum을 보면 아래와 같다.
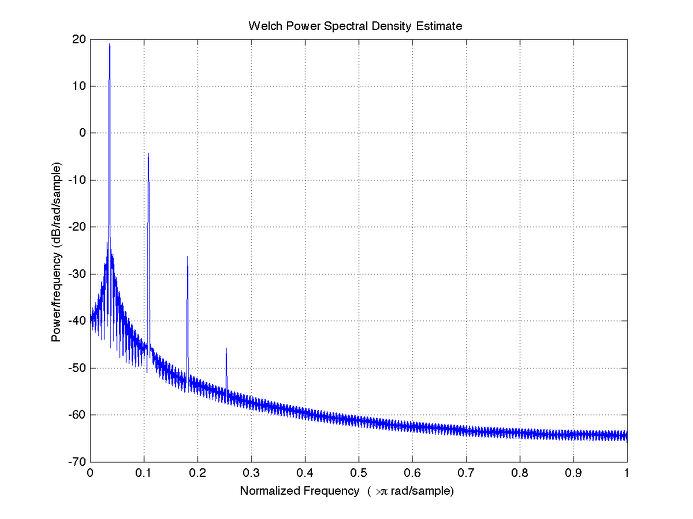
그림에서 보면 가장 높이 솟은 부분이 입력 신호의 주파수가 되고, 두번째가 2nd order harmonic, 그리고 3rd, 4th되겠다.
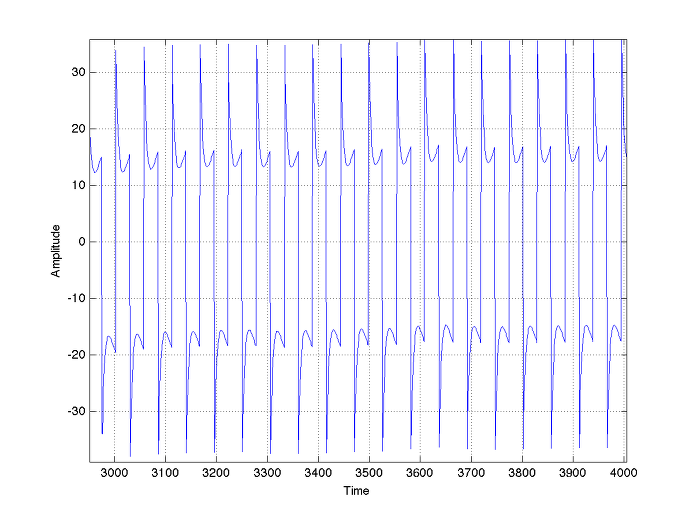
이때의 신호 파형은 아래 그림과 같다.
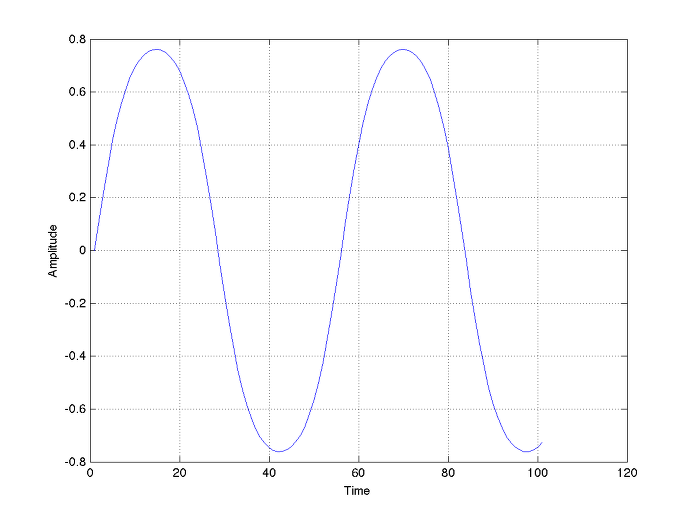
언뜻 보면 sine wave같지만 아래 위가 조금씩 눌려(compressed)있다. 이 정도 눌렸을 뿐인데, 3rd와 4th harmonic도 무시할 수 없을 만큼 있다. 네모 반듯하게 눌러버리면 더 이상 말할 필요가 없겠지.
Tube는 실제로 grid limiting current가 걸리는 +부분은 그림처럼 soft하게 뭉개지고, -부분은 cut-off에 의하여 네모반듯하게 뭉개진다. 증폭단을 거치게 되면 입력신호는 역상이 되는데 (아래 위가 뒤집어짐) 여러 단의 증폭단을 거치면 hard clipping 된 부분은 다음단에서 soft clipping을 맞이하게 되고 soft clipping 된 부분은 hard clipping되게 된다. 또 증폭단과 증폭단 사이에서 AC coupling/miller effect에 의하여 모양은 아래와 같아진다.
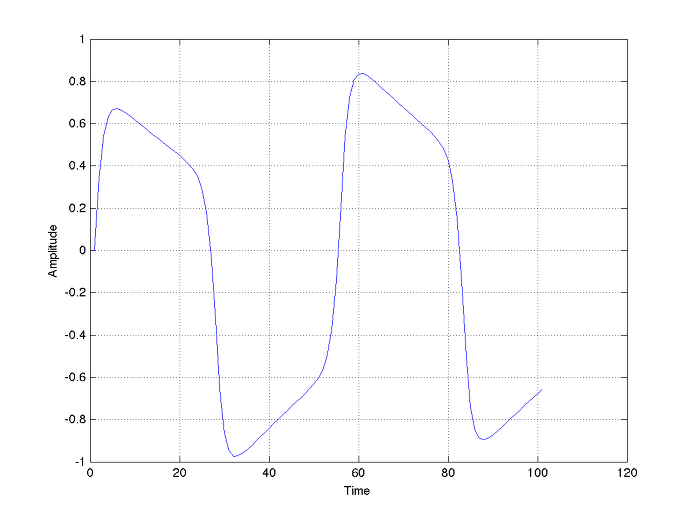
이러다 마지막 증폭단에 가게 되면 cut-off에 의한 부분은 그냥 네모나게 남아있고 여기에 tone stack을 거치게 되면 기본적으로 middle frequency range에 notch (푹파임)가 생기게 되어 신호 파형을 보더라도 그 유명한 Marshall notch (방형파 모양으로 깨진 모양에 양 끝 모서리가 뾰족하게 올라온 모양)가 되어 나타나게 된다. (아래 그림 참조)
종합하면 soft-hard-soft-hard clipping이 반복되면서 3rd-4th보단 2nd가 주로 늘어나는 방향으로 찌그러짐이 일어나고 매 증폭단에서 bandpass filtering이 일어나서 불필요한 저음과 고음의 하모닉을 깎아주어 지저분하지 않으면서도 풍부한 배음을 갖도록 만들어준다.
여러 날 시뮬레이션을 해보고 문헌들을 읽어봤지만, 사실상 프리앰프 시뮬레이터를 spice처럼 만들지 않는 이상은 정확하게 시뮬레이션하는 것이 불가능하고 더구나 현존하는 진공관 모델이 실제와 차이가 있기 때문에 가장 수고를 덜 들이면서도 높은 효과를 보는 것은 중요한 특성만을 잡아내어 갈고 닦는 방법 밖엔 없다는 결론을 계속해서 내리게 된다. 이 sigmoid function의 경우도 일본의 악기회사들이 그 옛날 많이 도입했었다고 한다. 알다시피 지금의 일본 악기들 대부분 실물 앰프와 비슷한 필은 얻어냈을지 몰라도 Axe Fx 급의 리얼리티는 많이 떨어진다. 제작비를 고려해서, 또 적당한 비용으로 구현을 하다보니 타협을 많이 했기 때문인데, 그렇다고 타협하지 않은 물건을 만들어내지도 못했다. 타협안하자면 가야할 길은 또 너무 멀기에..