디지털 세계에서의 디스토션과 aliasing

Written by Keith
on 
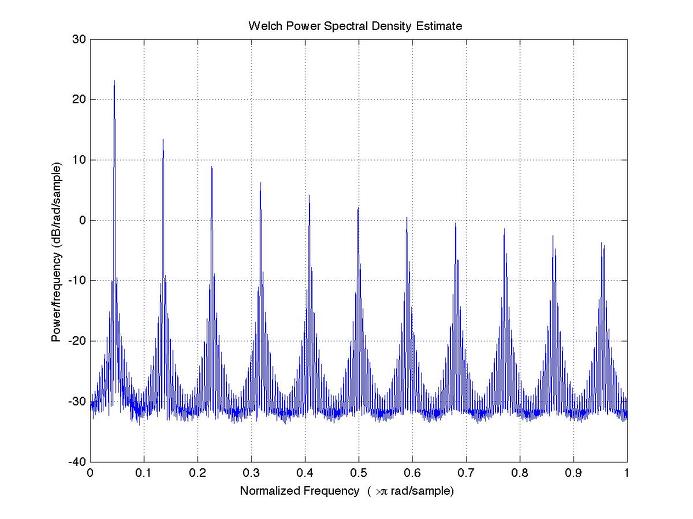
Featured image

흔히 aliasing이라고 하면 아날로그 신호가 디지털에 들어올 때 아날로그 신호의 주파수 대역 대비 샘플링 주파수를 너무 낮게 잡아서 높은 주파수의 신호가 낮은 주파수의 신호로 마치 미러링되는 것으로 이해할 수 있다. 즉, 내가 디지털 세계에서 처리할 수 있는 최대의 주파수를 A라고 할 때 이것보다 높은 B의 신호를 (필터링을 해서 깎아 버리지 않고)입력 받으면 B의 신호가 A주파수만큼 처리할 수 있는 시스템에서 엉성하게 관찰되어서 그것이 원래 처리해야 할 신호들을 방해하거나 오작동을 하게 한다는 말로도 해석할 수가 있다.

디지털 영역에서 saturation과 같은 비선형 조작을 신호에 가하면 마찬가지로 aliasing이 생긴다. 무슨 말이냐면 실제로 내가 설계한 시스템, 즉 가청 주파수만을 처리할 수 있도록 설계된 시스템에서라도 내부에서 비선형 함수를 써서 조작을 가하면 고차의 배음 (Harmonic)이 생겨나면서 이 harmonic이 내 시스템의 Nyquist frequency (sample frequency의 1/2)을 넘어가는 경우는 그것이 엉성하게 관찰되면서 다시 가청주파수 대의 신호로 들어오게 된다는 얘기다.

잘 이해가 안될까봐 그림을 몇 개 넣어서 설명해본다.

image44.1 kHz Sample Rate

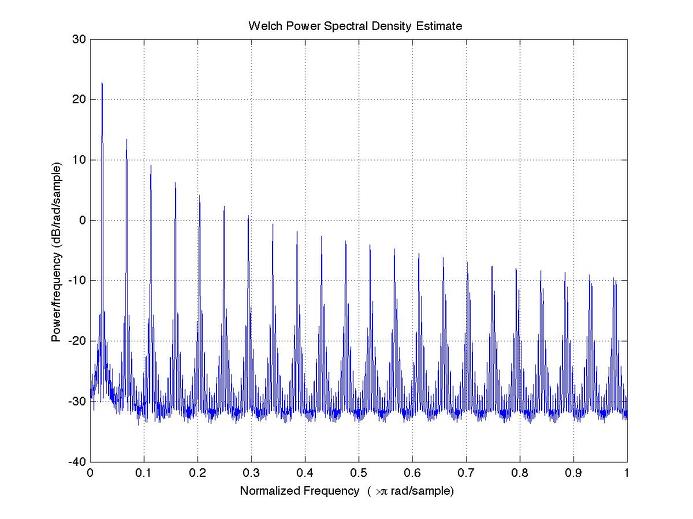image2x 44.1 kHz Sample Rate

44.1 KHz X2 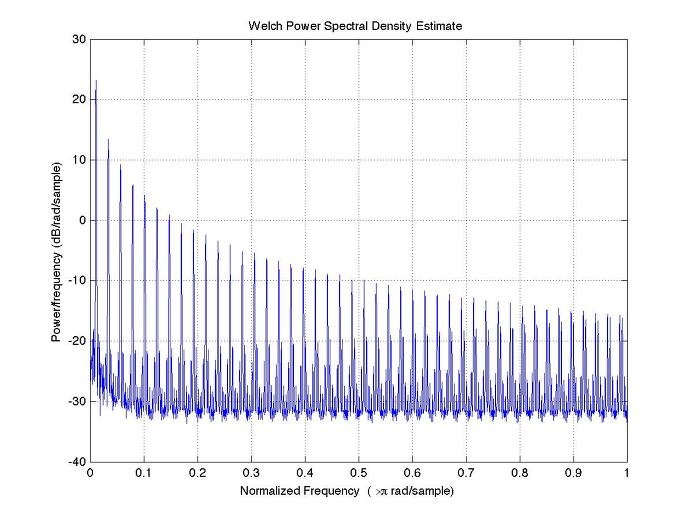image4x 44.1 kHz Sample Rate

44.1 KHz X4 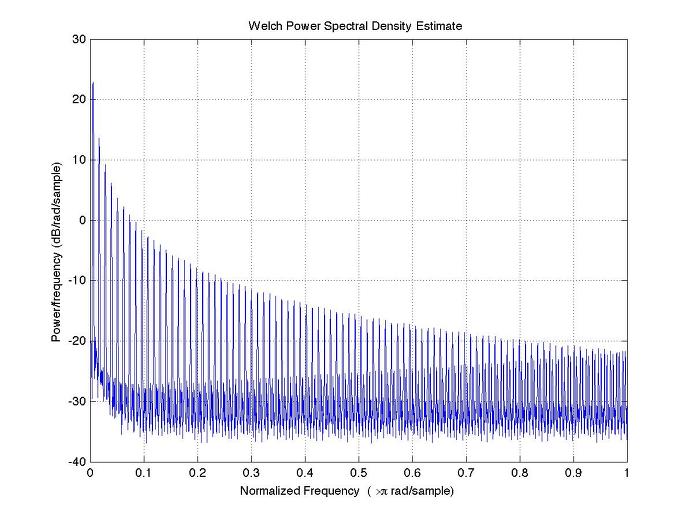image8x 44.1 kHz Sample Rate

44.1 KHz X8

위 그림들은 순수한 1kHz의 sine wave를 발생시켜 그것을 worst case의 clipping function인 sign function을 걸어주었을 때 샘플레이트를 달리해서 주파수 스펙트럼을 관찰한 것이다. sign function을 쉽게 해석하기 위해 taylor series로 전개시키면 입력의 1차 2차 3차 …의 합으로 나타나는데, 그 각 차수에 곱해지는 weight는 차수가 높아짐에 따라 점점 작아지는 경향을 보인다 (알다시피 그래서 대략 그 항이 매우 작아지면 미치는 영향이 작은 것으로 보고 적당히 끊어서 근사하기도 한다). Sine함수의 2차 3차 항들은 잘 알다시피 다시 써보면 고주파의 sine 함수로 바꿀 수가 있고, 그 얘기는 입력의 harmonic이 생겨난 것으로 이해할 수가 있는 것이다. 즉 비선형 함수를 series로 전개했을 때의 각각의 고차항은 그 차수에 비례하는 harmonic을 의미한다고 보면 된다. 그러나, sign 함수는 1차나 3차 함수의 모양에 가까운 함수이기 때문에 2차항보다는 홀수항, 즉 +입력에 +출력, -입력에 -출력을 내보내는 성분이 많을 수 밖에 없으니 사실상 홀수차항만 존재하게 될 것이다.

어쨌든 그렇게 놓고보면 찌그러짐을 경험한 신호는 그 하모닉이 갑자기 엄청나게 증가하게 되는데, 그것이 우리가 설계한 시스템(44.1kHz로 샘플한다고 하자)에서 허용하는 Nyquist frequency를 넘어서게 되면 aliasing이 일어나게 되는 것이다. 다시 말해 실제로 높은 주파수의 신호인데, 그것이 다시 낮은 주파수 신호로 관찰되어 간섭으로 존재한다는 의미가 된다. 간섭이 된다고 함은 의도하지 않은 애매한 주파수의 신호로 남아서 존재하기 때문인 것이다. 이를테면 1KHz의 입력에 대해서 홀수차항만 존재하게 되면, 3, 5, 7, 9, 11, 13, .., 21kHz까지의 harmonic만 남고 그 이상의 harmonic은 aliasing으로 남아서 23kHz는 22.1kHz를 중심으로 안쪽으로 mirroring된다고 할 수 있으니까, 22.05-(23-22.05)=44.1-23=21.1 kHz에 나타나고, 25 kHz는 19.1kHz에 나타나는 식으로 된다. 그렇게 주욱 늘어서다가 다시 44.1Hz을 넘어가면 0 Hz을 중심으로 + 방향으로 늘어서고..하는 식으로 하다보면 원하지 않는 harmonic들이 엄청나게 쌓여진다.

이것은 어디까지나 주파수 영역에서의 해석이고 시간영역에서의 해석은 sample rate가 크지 않아서 찌그러짐이 일어나서 변화된 모양을 세밀하게 표현하지 못하니 거기서 오는 불확실성에서 오는 문제라고 볼 수 있다. 다시 말하자면 샘플링 주파수가 높으면 날카롭게 깨져나간 모양을 세밀하게 묘사할 수 있는데, 그렇지 못하니 실제로 샘플과 샘플사이에 그 공간이 둥그런 것이었는지 날카로운 것이었는지 표현이 안되다보니 최대한 노력한 결과로 볼 수 있는 것이다. 다시 말해 낮은 차원에서 높은 차원에 어떤 것을 관찰하자니 자기 차원에서 할 수 있는 것은 다 동원한 상황이라고나 할까(뭐 이러한 해석도 있다).

추가적인 이해를 돕기 위해 사운드를 동원해 보았다. 파일 이름에 oversampling factor가 적혀있다. 적어도 2x oversample만 해도 뭔가 지저분하게 들리는 소리가 많이 줄어든다. 그것은 입력 신호의 주파수가 1kHz이기 때문이라고 보면 그것이 가청 주파수의 한계에 가까와지면 꽤 많은 oversampling을 해야함을 의미한다.

실제로 아날로그 세계에서는 샘플링 주파수는 무한대이고 아무리 높은 주파수의 harmonic이 존재한다고 하더라도 이것은 이미 얘기했든 진공관이 느린 소자라 기생 용량 성분에 의해서 많은 부분 다음 증폭단에 들어가면서 소멸이 되고, 어차피 살아남은 harmonic이라고 하더라도 1/2, 1/4주파수의 harmonic이 되지 않고 계속해서 고차항으로 늘어갈 것이고 결국 스피커에서 전부 잘려나가기 때문에 귀로 들릴 수가 없다.

따라서, 디지털 세계에서는 필요없는 harmonic이 생겨나기 전 sampling rate을 올려서 처리한 후모두 filter로 cut을 해서 down sample하거나, 아니면 아예 샘플 주파수를 높여서 처리하고 나서 downsample을 하든지 둘 중의 하나를 택해야 한다. 알다시피 over/down sample을 하는 과정(sample rate conversion)은 filtering을 하기 위해 많은 연산을 해야하니 자주 하는 것도 번거로운 일인데, 사실상 sample rate가 높을 때에 들어가는 filter의 수를 줄이면 sample rate을 계속해서 바꾸는 것보단 한번 바꿔서 모든 비선형 신호처리를 끝내고 다시 sample rate을 낮추는 것이 좋을 것으로 본다. 어쨌든 비선형 연산에 의한 aliasing을 커버하기 위해서 8배로 sample rate를 증가시키면 연산량도 그에 맞춰서 8배로 늘어나게 되는데다 sampling rate conversion에 필요한 여분의 연산까지 생겨나게 되므로 여기서 또 다른 의심은 생겨난다. ‘과연 실시간으로 제대로 모델링한 앰프 시뮬 플러그인이 있을까?’

대략적으로 문헌에서 정리되고 있는 것은 기타 신호는 대략 수백~10KHz 정도에서 왔다갔다하는 신호이니 일반적인 44.1kHz의 8배 oversampling을 하면 적당하다고 한다. 그 얘기인 즉, 8배로 관찰 시점을 늘리면 아무리 사나운 디스토션이라고 하더라도 그 날카로움을 표현하는데 문제가 없다는 것이고, 주파수 영역에서 관찰하면 aliasing에 의해서 간섭하는 성분들의 크기가 충분히 작은 값들이 된다는 말도 된다. 생각해 보면 과거에 사용하던 디지털 멀티 이펙터들이 소리가 지저분했던 것도 이 aliasing 때문이었다고도 생각해 볼 수가 있고, 그래서 ‘디지털’스럽다고도 했던 것 같다. 당시 이펙터가 충분히 작은 크기로 만들어져야 하니 샘플레이트도 높지 못했을 거고, 찌그러짐을 일으킬 때에도 이런 저런 필터를 붙여서 돌리려고 하는데도 노력이 많이 들었을테니 아마도 엄청나게 아껴가며 붙였을테니 말이다.

여기서 정리하면,

이상이다.