Accurate Plate Follower C Model (1)
on
회로 시뮬레이션을 한다고 할 때, 대부분의 선형회로의 경우는 이것을 손쉽게 1:1로 완벽하게 디지털 세계로 옮겨 놓을 수 있고,R/L/C 회로의 경우도 bilinear transform을 이용해서 완벽하다고는 할 수 없지만, 디지털 필터로 근사화가 가능하기 때문에 (귀가 속아주는 범위에서) 거의 완벽하게 옮겨 놓을 수가 있다.그러나, diode, Tr, tube, 또는 실제의 transformer와 같은 비선형 소자가 달라붙는 경우에는 이것의 특성이 완벽한 수식으로 나타나는 것이 아니라 실제의 일부 특성만을 curve-fitting한 비선형 함수로 나타나고, 회로 방정식을 풀 때 closed form의 solution이 얻어지지 않아 별 수 없이 수치해석적 방법을 도입하게 된다. 다시 말하자면, 모델의 원형도 근사화된 수식이고, 그것을 해석하는 과정도 점근적으로 이루어져서 쉽게 말하면 오차 덩어리라고 볼 수 있다.
그러나, 실제의 회로는 회로가 의도하지 않은 다양한 오차 (부품의 오차, 동일 부품 사용시 부품간 편차, 원하지 않는 외부 잡음 간섭 등등)를 가지고 있기 때문에 디지털 모델링 자체가 갖는 오차는 실제 회로의 오차의 평균값보단 작지않을까 하는 기대를 갖게 한다.
수치해석적이라 함은 방정식의 해를 단번에 구하지 못하니 예상치를 넣어보고 오차가 어느 정도니 다음에는 해와 더 가까운 지점에서 계산해보고 하는 일을 여러 번 반복해서 오차가 정해진 범위 내에서 해가 얻어지도록 계산하는 방법이다. 잘 알려진 방법이 Newton-Raphson (N-R)이며 Homotopy라고 해서 N-R이 해에 수렴하기 곤란한 조건을 위해서 사용하는 방법들이 있다. 어쨌든 여기서는 N-R 방법을 쓰기로 한다.
이것이 어찌보면 기타앰프 시뮬레이션의 발목을 쥐고 있다고 봐도 될 만큼, 정확도를 높이면 더 많은 연산을 수행해야되고 연산량을 줄이기 위해서 꼼수를 쓰면 정확도가 떨어지는 경향을 보게 된다.
- 초 간단 모델
C가 여기 저기 달라붙는 실제 회로에 도전하기 전에 R만 cathode/plate/grid에 달라붙은 회로에 도전하기로 한다.
N-R 방법으로 회로를 해석하는 방법은 다음과 같다.
1) KCL/KVL로 방정식 세우기
2) 초기값 설정 하기
3) 함수값 (f(x)) 계산 + 함수의 미분 값 계산 (f’(x))
4) N-R Iteration:
초간단 모델에서 X값은 plate/grid current를 얻기 위해 사용하는 Vgk, Vpk 값이 된다. 구체적으로 식을 세워 보면 다음과 같을 것이다.
5) 오차(=함수값)가 threshold이내가 되도록 iteration
어차피 함수의 미분값 또한 closed form으로 계산하기 어려우므로 매우 작은 delta에 대해서 기울기를 계산한다.
즉,
이렇게 얻어진 회로 변수들 (node voltage, branch current)등은 사실상 거의 참값으로 놓아도 무방하다.
실험 결과로 얻어진 그림을 몇 가지 붙여 본다.
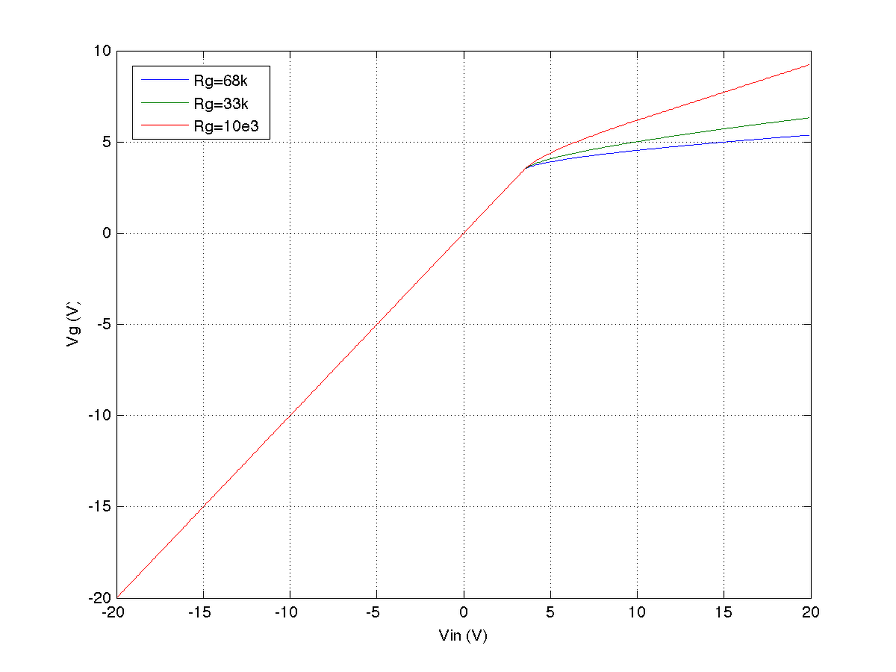
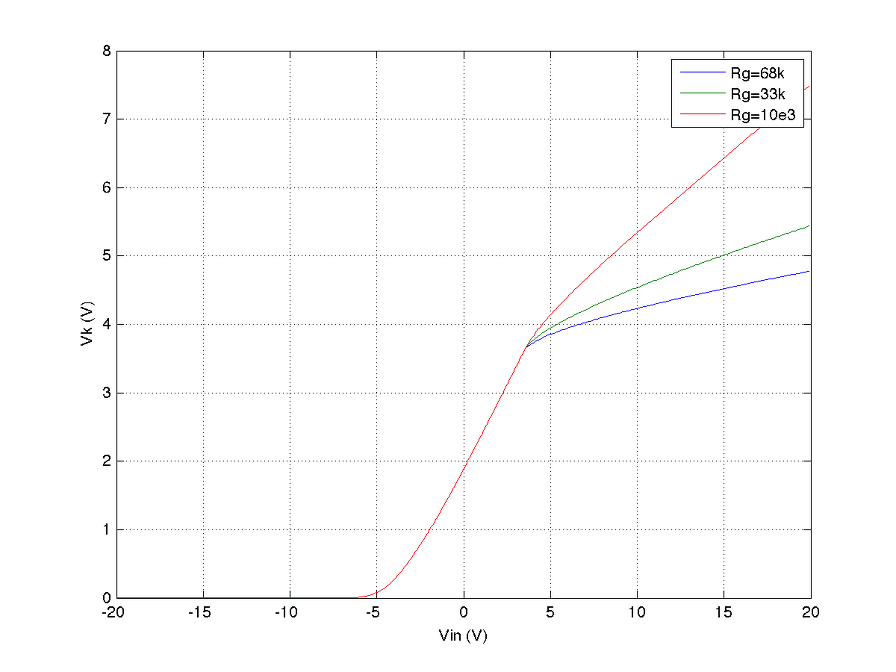
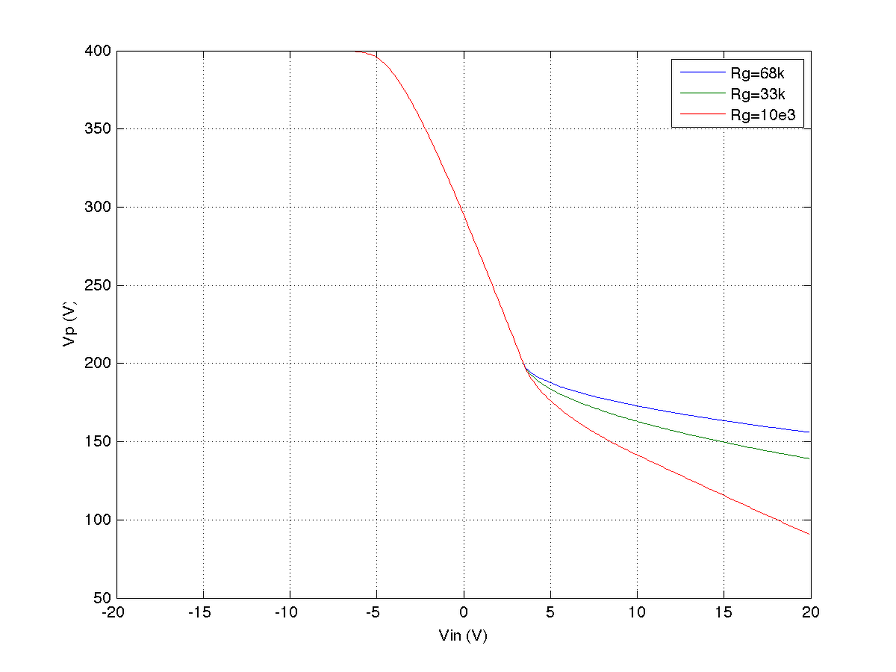
Rg=68k, 33k, 10k로 변화시키고 Rp=100k, Rk=1.8k로 놓았을 때의 Vg, Vp, Vk의 그래프를 각각 그린 것이다.

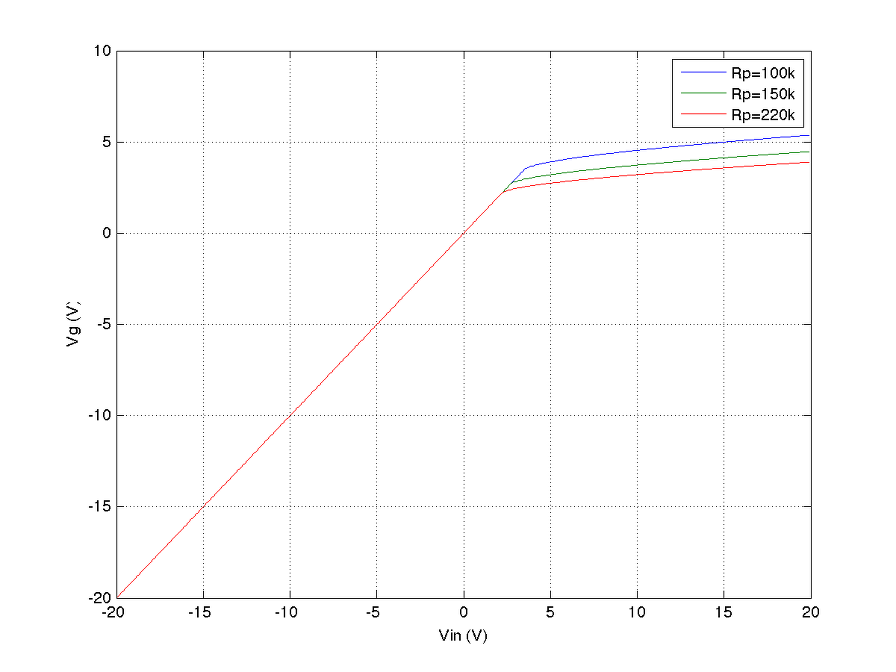
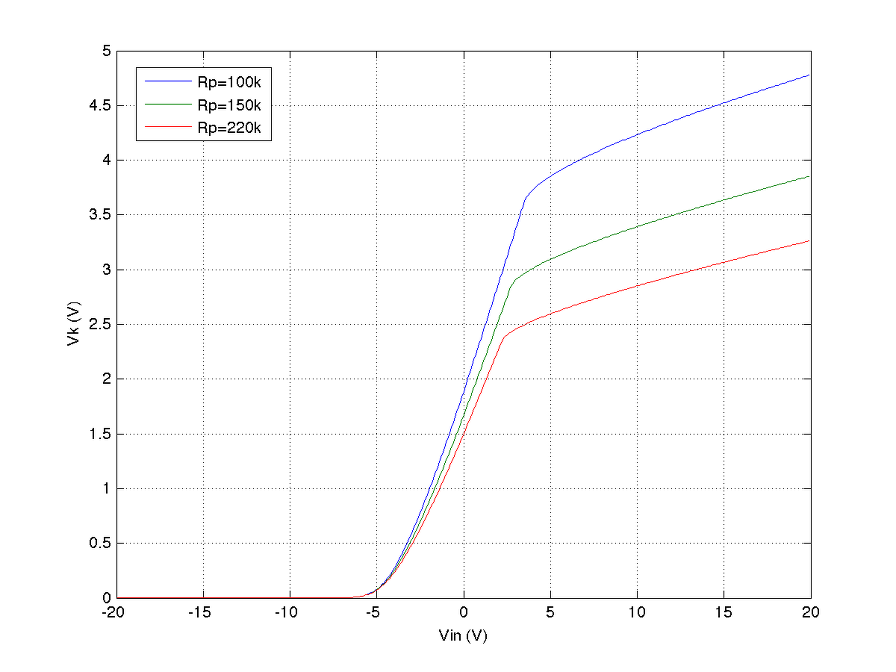
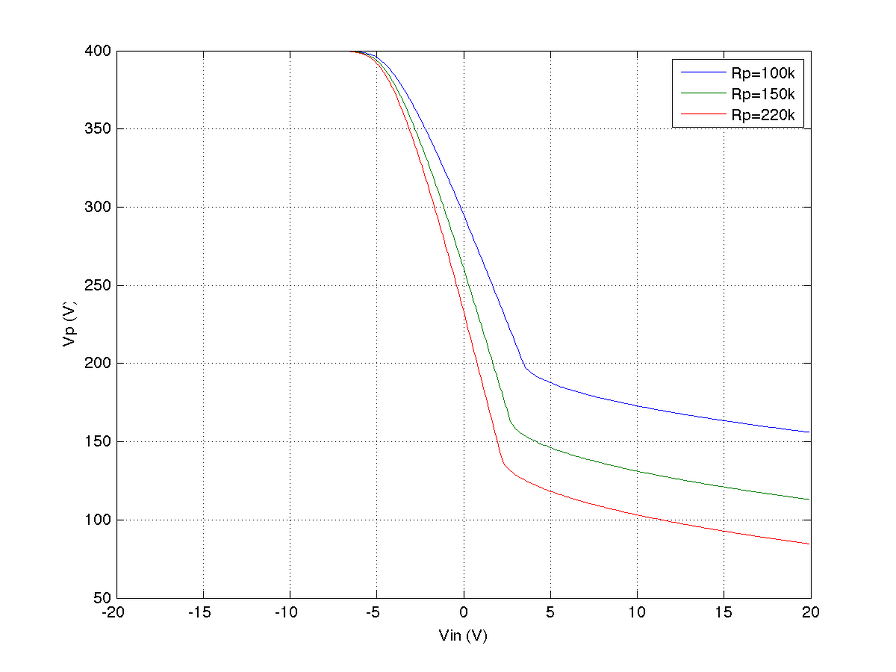
다음은 Rp를 100k, 150k, 220k로 바꾸었을 때의 특성을 시뮬레이션 한 것이다.
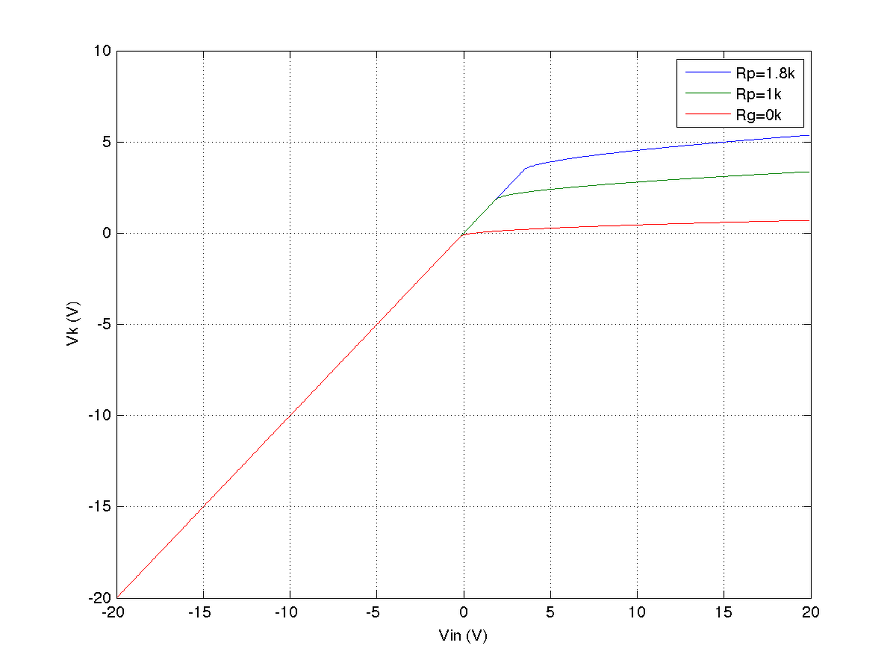
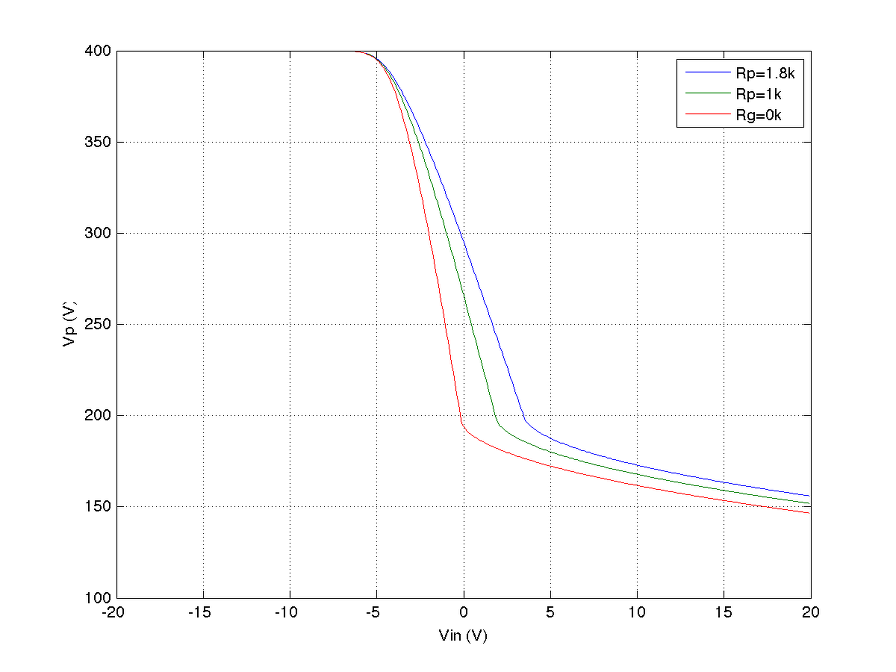
다음은 Rk=1.8k, 1k, 0k로 바꿔 가며 실험한 결과이다.
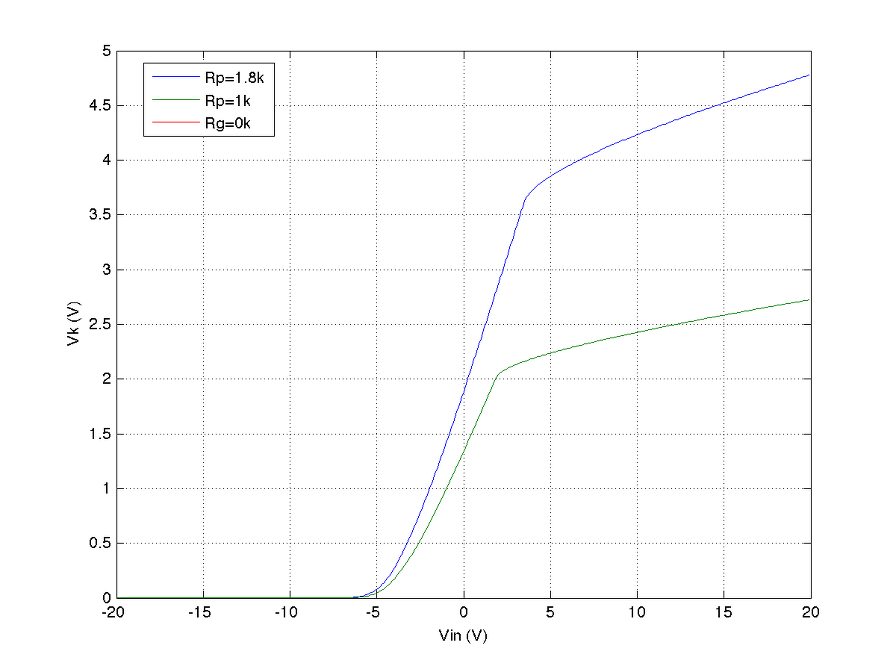
C를 통해 간단히 시뮬레이션 한 것이지만 사실상 Spice를 써서 얻은 결과와 같다고 볼 수 있다.
다음 포스팅에서는 C가 달라붙는 본격적인 회로의 시뮬레이션을 다뤄보기로 한다.
- 고찰해 볼 내용들
위 그래프는 사실상 Plate Follower의 기본적인 특성을 나타내는 곡선들로서 각각이 시사하는 바가 나름 크다고 볼 수 있다. 위 그래프를 모두 이해하면 나머지는 일종의 부가 상식이라 기타 프리앰프를 훨씬 더 쉽게 이해할 수 있다.
소신호 모델을 이용한 기타 시뮬의 경우 증폭률 상수로 전 영역에 적용하고 양 끝단의 voltage를 threshold로 하여 찌그러짐을 얻어내는 방식을 쓴다. 그러나 그래프에서 볼 수 있듯이 cut-off에 의한 찌그러짐과 grid limitting current에 의한 찌그러짐은 확연히 다른 모습을 보여주고 있음을 알 수 있다. (이후의 포스팅에서는 다양한 모델들을 적용했을 때 발생하는 오차들에 대하여 알아볼 것이다.)
특히 grid limting current의 특성은 grid resistor가 어떤 값이냐에 따라 크게 부각되기도 하고 덜 부각되기도 하는 것을 알 수 있는데, grid resistor가 작은 값일 수록 voltage drop이 작으므로 사실상 grid의 찌그러짐이 덜 부각되고 resistor가 큰 값일 수록 voltage drop에 의한 grid limiting current 유입은 줄어드는 반면 찌그러짐은 더 부각되는 것을 확인해 볼 수 있다. 대부분의 진공관 회로가 그렇듯, 출력 임피던스가 높고 그 높은 출력 임피던스는 등가화하면 grid resistor로 반영된다. 따라서, grid limiting current에 의한 찌그러짐은 1) cut-off에 의한 찌그러짐처럼 덜 soft할 수 있고, 2) grid를 통한 전류 유입양이 상대적으로 작아져서 매 증폭단을 discretization하더라도 그 효과는 상대적으로 미미해질 수 있는 여지를 보여주고 있다.
여러 그림에서 보여지다시피 grid resistor는 대부분의 경우 앞단 회로를 전압원과 출력임피던스로 등가해보면 수백 kohm에 이르고 있는데, 이러한 경우 사실상 hard한 clipping을 얻게 되고 grid current 유입도 매우 작아지게 되므로 상대적으로 간단하게 모델링 될 수 있고 그 오차도 상대적으로 작을 것으로 예상된다.