모노를 스테레오로 만들어보기

모노를 스테레오로 바꾸는 방법에는 여러 가지가 있는데, 그중 가장 대표적인 것은 모노 소스를 주파수 상에서 빗처럼 촘촘한 필터 (이것을 comb filter라고 함)를 이용해서 두 부분으로 분리하고 그것을 좌우에 배열하는 방법이다. 이 둘이 서로 겹치지 않게 해야 스테레오의 효과가 살아난다. 기본적으로 알아두어야 할 것은- 스테레오 소스가 아닌 모노 소스는 사실상 정보량이 1/2인 것이라 강제로 스테레오처럼 들리게 해도 그 (음장감의) 단순함은 피할 길이 없다.- 보컬이라든가 솔로 악기는 대개 여러 번 녹음하지 않는 이상 모노 소스라고 봐야한다. 다만 스테레오로 들리게 처리했을 뿐이다. 문제는 필터 1의 출력은 좌측으로 필터 2의 출력은 우측으로 놓는 게 아니라 이 둘을 서로 계속해서 바꿔치기해야 귀로 듣기에 모노가 아니라 스테레오인가 속아넘어갈 수 있기 때문에 계속해서 바꿔준다. 이 방법을 코러스처럼 VCO가 진동하듯 어떤 주기에 따라 서서히 바꿔치기 할 수 있기도 하고 아예 서서히 랜덤하게 바꿔치기 할 수도 있다. 말이 바꿔치기지 comb filter의 특성을 주기적으로 (귀가 눈치 못 채게) 계속해서 바꿔준다는 의미가 더 맞겠다. Comb filter는 무슨 구조를 가지고 있길래 마치 촘촘한 빗처럼 어떤 주파수 성분은 통과시키고 어떤 주파수 성분은 안통과시키고 할 수 있는 것인가 궁금할 수 있겠다. 주파수 영역에서 복잡한 필터는 시간 영역에서 바라보면 오히려 간단해지는 경우가 있는데, 이 경우가 그렇다. $x(t)$라는 모노 소스가 입력되었다고 할 때, 여기에 시간 $\tau$만큼 지연된 신호 $x(t-\tau)$가 $\alpha$만한 크기로 더해졌다고 하면, 출력은 다음과 같이 쓸 수 있다. \(y(t) = x(t) + \alpha x(t-\tau),\) 이것을 주파수에 대한 수식으로 전부 트랜스폼해버리면 다음과 같아지므로, \(Y(\omega) = X(\omega) + \alpha X(\omega) e^{j\omega \tau} = (1+e^{j\omega \tau}) X(\omega) ,\) 필터의 주파수 응답은 다음과 같아진다. 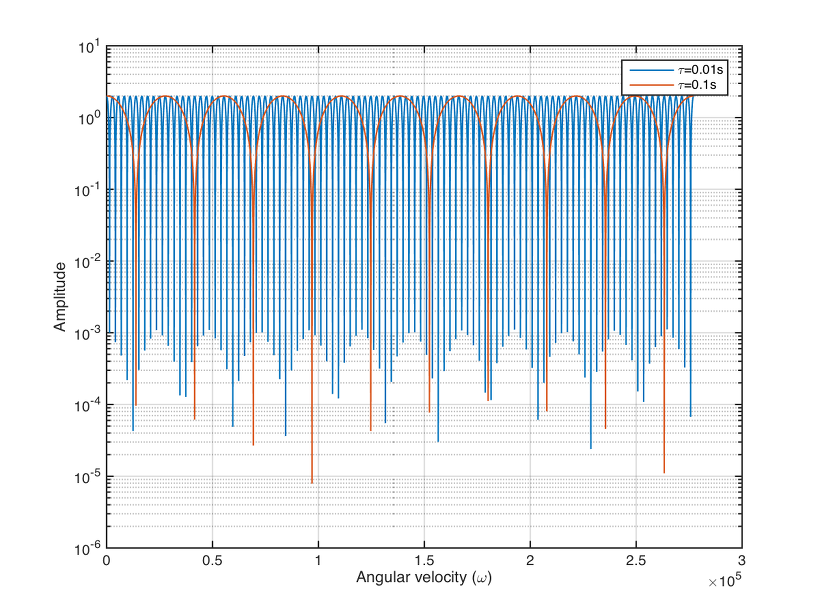\(H(\omega) = 1+\alpha e^{j\omega \tau},\) 식을 대략적으로 보면, $\alpha$의 값과 $\tau$에 따라 comb filter의 모양, 촘촘함이 결정될 수 있음을 알 수 있다. $\omega \tau$가 정확하게 $\pi$ 값을 가지게 되면 filter의 응답이 0이 되므로 모든 신호가 지워지고, 반대로 $2n\pi$가 되면 최대가 됨을 알 수 있다. 여기서 위상을 좀 틀어주면 최소/최대가 되는 지점이 달라지게 된다. 그림으로 나타내면 다음과 같다.

결국, 두 개의 comb filter를 사용하되 시간 지연 정도와 시간 지연 성분의 위상 값을 다르게 하면 재미난 결과를 얻게 되는데, 그렇게 해서 생겨난 이펙트가 phase shifter나 flanger, chorus, stereo enhancer 등등이 되시겠다. 조작할 수 있는 값이라든가 방법은 다양하지만 그것을 귀로 들었을 때 맘에 드는 소리가 나는 조합을 찾는 것은 쉽지 않다.이것은 예전에 언급했던 Haas effect, 즉 귀로 도달하는 신호가 서로 같은 진폭으로 약간의 시간차를 가지고 들어오고 있다고 할 때, 그것의 차가 어느 수준 이하이면 우리는 그것을 서로 시간 차가 있는 두 개의 소리를 듣고 있다고 생각하지 않고 어떤 방향에서 신호가 오고 있다고 느끼게 된다고 했다. 이것을 바탕으로 생각해보면, 이러한 스테레오 이펙트를 준다는 것은 하나의 입력 신호가 정 중앙에서 들려오고 그것의 일부 혹은 카피본이 좌우로 어떤 패턴을 가지고 또는 랜덤한 패턴으로 심하게 왔다갔다 움직이는 경우처럼 들린다는 것이다. 우린 그걸 스테레오 음상으로 알아듣는단 말도 된다. 좀 더 신기한 것은 시간차를 가지고 있고 그 시간차가 시간에 따라 변화한다고만 해서 스테레오로 듣는 것이 아니라 일정 조건을 만족해야만 그렇게 들리고 그게 잘 들어맞지 않으면 어색하게 들리게 된다는 것이다.중요한 것은, 우리가 다루는 많은 소스들이 대부분 모노이고, 스테레오 소스라고 하더라도 원래 모노였는데 스테레오로 가공된 것들이다. 우리 실상의 스테레오라고 하는 것은 그저 어떤 공간에 마이크 두 개를 가져다 녹음하는 것이 전부다. 소리를 만들어내는 개개의 음원들은 그것이 스테레오 오디오가 아닌 이상엔 스테레오 음향을 만들어주진 않는다. 그래도 우리가 스테레오라고 생각하게 되는 것은 주위의 잡음이 몹시 랜덤해서 두 개의 마이크로 같은 소리로 잡히지 않고, 음원으로부터 출발한 소리도 다양한 주변 물체들에 반사된 소리들과 한꺼번에 들리기 때문에 양쪽 귀에 완전히 같은 소리로 들어오지 않기 때문이다. 스테레오 이펙트, 즉 pseudo stereo, 강제로 모노 음원을 스테레오 음원으로 만드는 작업은 위에 설명한 대로 단순한 덧셈 뺄셈, 위상천이를 이용해서 만들 수도 있지만, 바로 위에 설명한 대로 가상의 공간을 꾸미고 그 공간에서 음파가 전달되는 것처럼 시뮬레이션하는 경우도 있다. 이것을 Spatializer라고 하는데, 과거에 오디오 프로세싱 용으로 나온 Spatializer라는 장비와 혼동을 일으키기 충분하다. 이 장비는 스테레오 음장감을 좌우로 더 벌려놓는 (Haas effect를 이용한 것으로 보여진다) 기능을 한다.보다 더 근사한 이펙트는 3D 가상현실에서 HRTF를 이용한 경우인데, 이것 나름대로 설명이 복잡해지니 여기까지 한다.